We want our watermelons juicy, sweet and smooth. Juiciness and sweetness are obvious qualities, but smoothness is also highly commendable. Smoothness is about the skin of the watermelon: when we hold them and caress them, we want to feel a firm, slightly humid skin, without any irregularities or soft spots. Of course!
In our watermelon farm, workers pick the watermelons when they are ripe and carry them to the production plant, where the watermelons are sorted and controlled for quality and smoothness. These operations are entirely automatic. The watermelons travel on a conveyor belt and are scanned by a robotic camera. Those who are perfectly smooth pass and those who are not are destroyed by a powerful laser beam that makes them explode (not a nice view, I can tell you …)
You are called to write the program that analyses the video image, identifies the unsmooth watermelons, directs the laser beam at them and fires.
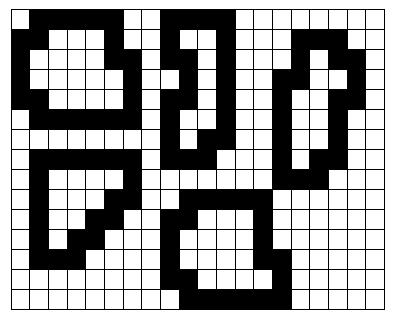
Your task is to write a program that reads from the standard input the description of an image of the watermelons on the conveyor belt and identifies those that are not smooth. On the image, only the contours of the watermelons are displayed. Each contour is a sequence of connected squares in a grid, which approximates the actual contour. Each square is connected to exactly two other squares, which lay (each of them) either on the same row or in the same column as itself. The following figure represents an image with five watermelons.

Mathematically, the criteria for smoothness of a continuous closed curve could be explained by taking the tangent to each point of the curve, starting at a some point, and moving clockwise (or counterclockwise) along the contour. If the watermelon is smooth, the slope of the tangent would decrease until minus infinity, and then decrease from plus infinity to minus infinity again and then and finally decrease from plus infinity until the initial value at the initial point. This is if we go around the contour in the clockwise direction. If we go counterclockwise, the slope increases to plus infinity, then from minus infinity to plus infinity, etc. Note that we are being informal: if the tangent does not exist, then the curve is not smooth; and “decrease until minus infinity” does not mean that the slope strictly decreases: it may remain constant for a part of the curve that is perfectly straight. In other words, again informally, what we mean is that from one point to the next (so to speak …), the slope of the tangent either decreases or stays the same. The same applies, mutatis mutandis, when we go counterclockwise (and the slope increases).
On a ragged contour, like the one in the image, we replace the slope of the tangent by the slope of segments taken along the contour. Let p1, p2, p3, …, pN, be the N points in the contour where the contour changes direction (either from horizontal to vertical or from vertical to horizontal). Then instead of an infinite number of tangents we only have to consider the n segments defined by the points <p1, p3>, <p2, p4>, …, <pN−1, p1> and <pN, p2>. If the slopes of these segments behave as the tangents in a curve then the watermelon is smooth. Otherwise it is not and should be destroyed. The figure below shows the contour of one of the watermelons from first figure and displays the segments that represent the tangents.

Each input file represents the image of set of melons on the conveyor belt. The first part of the input file contains two integers, representing the number of rows, R, and the number of columns, C, in the image. Exactly R lines follow, each line having exactly C characters. Each character is either ‘M’, representing a square in the contour of one watermelon, or ‘-’ (the minus sign) for all other cases (squares either inside or outside contours). If there is an ‘M’ in the position <x, y> (column x, row y), then exactly two of the four positions <x+1, y>, <x, y+1>, <x−1, y> and <x, y−1> also contain an ‘M’. Thus, each ‘M’ belongs to a closed contour. All positions inside such a contour contain a minus sign. Note that watermelons can touch each other at corners, as exemplified in the first figure.
The output contains one line for each unsmooth watermelon, displaying the horizontal and vertical coordinates of the center of the watermelon, or the message “ALL SMOOTH” (in uppercase, without the quotes) if all the watermelons are smooth. The lower left corner has coordinates <0, 0>. Horizontal coordinates grow rightwards and vertical coordinates grow upwards. The horizontal coordinate of the center of the watermelon is the average of the horizontal coordinates of all the dots in the contour, and likewise for the vertical coordinate. This average is computed using integer division. Theoretically, the center of a watermelon may lie outside the contour, in which case the laser beam will fail to blow out the watermelon, but such a bizarre watermelon has never been seen in nature. The pairs of coordinates are to be sorted by the vertical coordinate and then (in case of a tie) by the horizontal coordinate.
15 20 -MMMMM--MMMM-------- MM---M--M--M---MMM-- M----MM-MM-M---M-MM- M-----M--M-M--MM--M- MM----M-MM-M--M--MM- -MMMMMM-M--M--M--M-- --------M-MM--M--M-- -MMMMMM-MMM---M-MM-- -M----M-------MMM--- -M---MM--MMMMM------ -M--MM--MM---M------ -M-MM---M----M------ -MMM----M----MM----- --------MM----M----- ---------MMMMMM-----
10 2 15 9 9 10
9 17 ---MMM-----MMM--- --MM-MM----M-M--- -MM---MM---MMM--- MM-----MM-------- M-------M---MMMMM MM-----MM--MM---M -MM---MM---M---MM --MM-MM----MMMMM- ---MMM-----------
ALL SMOOTH
This document was translated from LATEX by HEVEA.