Lego Mosaics

Building mosaics is an art dedicated to the construction of images by assembling small pieces of some material. Lego pieces are all about building things by assembling small pieces, and therefore they present the flexibility and versatility to create wonderful mosaics.

You have been commissioned to build a large lego mosaic. The basic idea is to use a lego plate and on the top of it attach some lego bricks. Each lego stud is like a pixel in the image. If we used text to represent a mosaic, with ’.’ representing a stud without a brick, ’R’ for a red brick, ’Y’ for a yellow brick and ’G’ for a green brick, then the mosaic of the image below would be represented by:

................ ......R......... ................ ..R.R.R.R.R.RRR. ..RRR.R.R.R.R.R. ..R.R.R.R.R.RRR. ..R.R.R.RRR.R... YYYYYYYYYYYYYYYY YYYYYYYYYYYYYYYY ...GGG.GGG.G.G.. .....G.G.G.G.G.. ...GGG.G.G.G.G.. ...G...G.G.G.G.. ...GGG.GGG.G.G.. ................ ................

For the construction of the mosaic you have available a very large set of 1×N bricks. In particular, for the purposes of the mosaic, you can assume you have an infinite number of 9 different types of bricks (in any needed color). These are 1×1, 1×2, 1×3, 1×4, 1×6, 1×8, 1×10, 1×12 and 1×16 bricks, and are depicted in the figure on the right.

For aesthetically reasons, you only want to use the bricks in the horizontal positions, that is, parallel to the bottom of the plate. This means that when seen from the top, as in the textual representation above, the width of the bricks is variable, but the height is always 1.

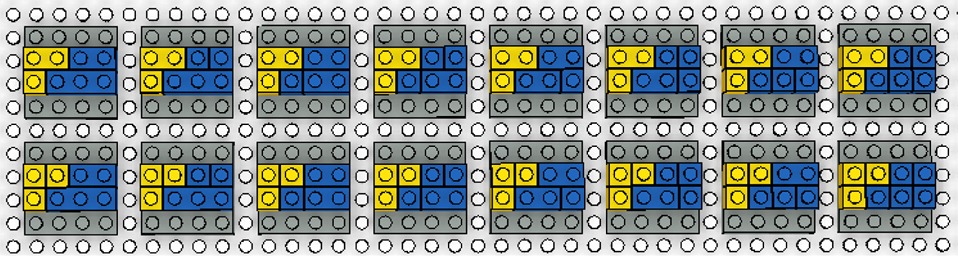
When you were starting the construction, you noticed that even with those constraints, there were several different ways of building the mosaic. For example, the mosaic below has 16 different ways of using pieces to obtain the exact same image (with ’B’ meaning a blue brick):

.... YYBB YBBB ....

Task

Given the description of a lego mosaic, your task is to compute in how many different ways you can build that mosaic assuming you have an infinite pool of 1×1, 1×2, 1×3, 1×4, 1×6, 1×8, 1×10, 1×12 and 1×16 lego bricks, in any color. The bricks must be positioned in horizontal positions.

Input

The first line of input contains two integers R and C, indicating respectively the number of rows and columns of the mosaic to be built.

The next R lines of input contain each exactly C characters detailing the mosaic to be built. Each character must either be ’.’ (representing a stud without any brick on top of it) or a capital letter (from ’A’ to ’Z’) representing a stud of a given color. Two bricks with the same letter representing it have the same color. You can assume that there is at least one brick in the mosaic.

Output

The output should consist of a single integer W indicating the number of ways in which the mosaic can be built, given that you can only use bricks of type 1×1, 1×2, 1×3, 1×4, 1×6, 1×8, 1×10, 1×12 and 1×16 on horizontal positions. You can assume you always have enough bricks to build the mosaic using any combination of the bricks you need.

Constraints

Input example 1

4 4
....
YYBB
YBBB
....

Output example 1

16

Input example 2

3 6
GGRRRR
GYYRRR
GGRRRR

Output example 2

2048

This document was translated from L^AT_EX by H^EV^EA.