Prince’s Highway

The main highway in the Algarve is Via do Infante. It used to be free but not anymore, because the Portuguese government decided to charge tolls on all motorways. Most users were unhappy, other fiercely objected to this measure, but a creative group of drivers came up with a clever idea, that, if implemented, might raise enough money to cover road maintenance and other operating costs, thus allowing Via do Infante to remain free. The idea is to rent the road pavement for advertising. Each side of the road has two lanes. If we take a straight part of the road, then we could rent either lengthwise rectangles, along a single lane, or widthwise rectangles, across the road, covering both lanes. Each of these rectangles could contain a floor poster advertising some product or some company, thus providing a nice source of income that could avoid charging those atrocious tolls. For reasons of economy of scale, all rectangles must have the same area.
The question is: in a given stretch of the highway, how many different ways are there to cover the pavement with such rectangles?

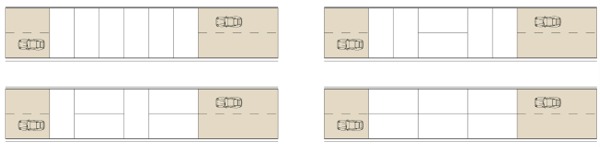
For example, the figure below illustrates 4 of the 13 ways of covering a pavement of length 6 with 2-by-1 rectangles.

Task

Your task is to find how many ways there are to fill a N-by-2 rectangle with 2-by-1 rectangles.

Input

The input file contains only a line with a single integer, N, representing the length of the stretch of the highway we are interested to rent for advertising.

Output

The output file contains a single line displaying the number of different ways of covering the given stretch of highway with 2-by-1 rectangles.

Constraints

• N > 0
• In all test cases, the result will not be larger than 2³¹−1.

Input example

42

Output example

433494437

This document was translated from L^AT_EX by H^EV^EA.